TCP 重转机制、滑动窗口、流量控制、拥塞控制（上）

大家好，我是小北。

我们都知道，互联网本质上是一个不可靠的网络环境，数据包在传输过程中可能会丢失、重复、乱序或损坏。

所以TCP就像一个非常靠谱的快递员，设计了一系列的"防呆"机制来应对这些问题。

这些机制包括：重传机制（包裹丢了就重新送）、滑动窗口（一次多送几个包裹提高效率）、流量控制 5800（收件人太忙就先放慢发货）和拥塞控制（快递车太多造成交通堵塞就绕道送，或者降低发货速度）。

而这篇文章就将深入探讨 TCP 的四大核心机制：重传机制、滑动窗口、流量控制和拥塞控制。

这些机制相互配合、缺一不可，共同保证了 TCP 传输的可靠性和效率。

一、TCP 重传机制

1.1 为什么需要重传机制

在计算机网络中，数据包的丢失是不可避免的，有很多原因都会导致丢包：

• 网络拥塞导致路由器缓冲区溢出，丢弃数据包
• 信号干扰导致数据包损坏，接收方校验失败后丢弃（checksum 校验失败）
• 路由器故障或链路中断导致数据包未能到达目的地
• 接收方处理能力不足，来不及处理而丢弃数据包

TCP 丢包的场景

为了应对各种情况，TCP 需要能够检测到丢包，并重发丢失的数据包。

那么 TCP 发送方如何判断丢包了呢？

答案是确认应答机制（ACK）

TCP 通过确认应答（ACK）和超时重传这两种基本机制来实现可靠传输。

1.2 TCP 确认应答（ACK）

什么是确认应答？

1. 发送方发送数据时，为每个数据段分配一个序列号（Sequence Number）

2. 接收方收到数据后，返回一个确认号（Acknowledgement Number），表示期望收到的下一个字节序号

3. 发送方通过接收到的确认号，可以判断数据是否已经成功到达接收方

TCP 基本 ACK 机制

如上图所示，

• 发送方先发送第一个数据包：

  • 序列号 SEQ = 100，长度50字节，也就是发送了100 到 149 这段数据

• 接收方收到后回复：

  • ACK = 150，意思是"我收到了100-149 的数据，请发送150 开始的数据"

• 发送方继续发送第二个数据包：

  • 序列号 SEQ = 150，长度50字节，也就是发送了150 到 199 这段数据

• 接收方再次回复：

  • ACK = 200，意思是"我收到了150-199 的数据，请发送 200 开始的数据"

当然，上图简化为一方发送，另一方接收数据，实际上 TCP 是全双工协议，双方可以同时发送/接收，同时发送时，ACK 就携带在数据包中。

1.3 TCP 超时重传

上面的例子展示的是理想情况，但网络是不可靠的，数据包在传输过程中可能会出现两种问题：

• 数据包丢失
• ACK 确认包丢失

如何解决这个问题呢？

对，就是超时重传：在发送数据包之后启动一个定时器，如果在指定重传超时时间（RTO, Retransmission Timeout）没有收到 ACK，就认为数据包丢失了，需要重新发送

超时重传两种情况

看到这，我们很自然的想到，超时重传机制有一个关键的参数：RTO（Retransmission Timeout，超时重传时间），RTO 的选择是个非常难的问题，过长或者过短都有问题：

• RTO 太短：可能导致不必要的重传，浪费带宽
• RTO 太长：丢包后等待时间过长，影响传输效率

TCP RTO选择问题

如上图中左图展示了 RTO 过短的问题：

• 发送方发出数据包后，在等待时间(RTO)过短就判定包丢失，导致发送方过早进行了重传
• 而原始数据包的确认(ACK)实际后面才到达，这种情况会造成不必要的重传，增加网络负担

右图展示了 RTO 过长的问题：

• 当数据包真实丢失时，发送方等待时间过长
• 虽然实际发送方收到重传包的 ACK 只需要较短时间(RTT)，但由于 RTO 设置过长，导致重传不及时，这种情况会降低网络传输效率

理想的 RTO 应该略大于网络往返时间(RTT)，既要避免过早重传，也要保证丢包时能及时恢复。

并且 TCP 的 RTO 不能设置为一个固定值，你想想上海到杭州的网络延迟和上海到纽约，那显然差距很大，所以 RTO 必须是动态调节的，以适配不同的网络链路情况。

那 RTO 的设置总要有个基本的参照物吧？

这个参照物就是发送方和接收方之间的实际网络延迟：

RTT（Round-Trip Time）：数据包从发送到收到确认 ACK 的往返时间

RTT 示意图

RTT 和 RTO 的关系

看到这，其实 RTO 和 RTT 的关系也就比较明确了：

RTO 应该适当大于 RTT

就像妈妈叫你去商店打酱油，你从家里到商店再从商店回来需要 RTT，如果你没及时回家，那妈妈至少要等 RTT 过后，才能再叫你爸爸去看看你咋回事了吧。

**那 RTO 到底取多少呢？ **

直接取RTT 吗？ 但是 RTT 是动态变化的呀，每个数据包的 RTT 可能都不一样。

TCP RTO 计算：RFC 793

在最早的 TCP RFC 793中，实际上并没有给出具体的标准计算方法，倒是有给出一个参考示例：

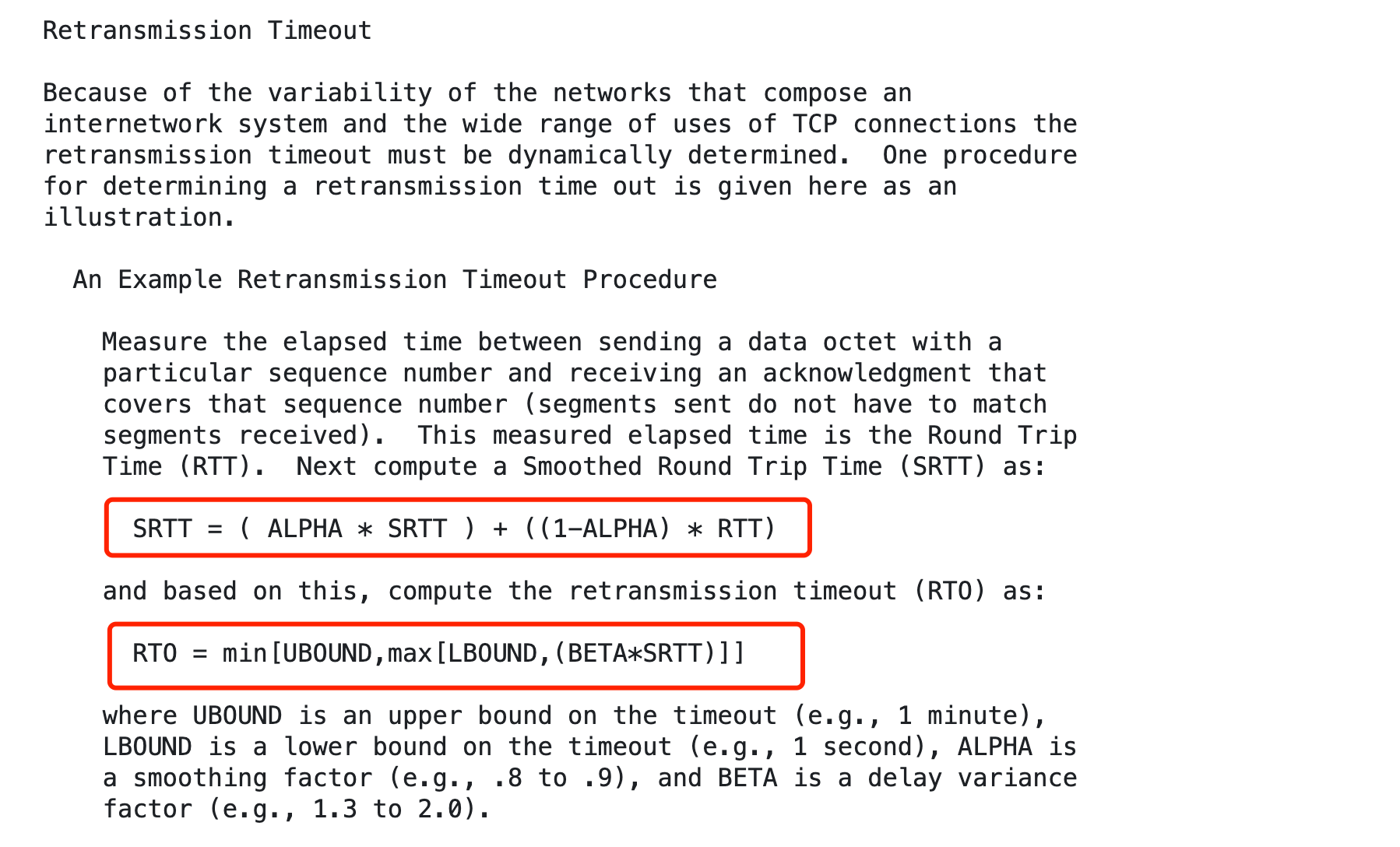
SRTT (Smoothed Round-Trip Time)是指 平滑的往返时间

具体公式说明:

• **SRTT = (Alpha * SRTT) + ((1-Alpha) * RTT) ** // 平滑RTT计算
• **RTO = min[UBOUND, max[LBOUND, (Beta * SRTT)]] ** // RTO计算

步骤：

• 先测量RTT：发送数据到收到对应 ACK 的时间间隔
• 然后计算SRTT：使用平滑因子计算平滑后的RTT
• 最后确定RTO：基于SRTT计算，同时考虑上下界

参数说明：

• Alpha：平滑因子，推荐值0.8~0.9
• Beta：延迟变化因子，推荐值1.3~2.0
• LBOUND：超时下限，建议值1秒
• UBOUND：超时上限，建议值1分钟

如果对于数学敏感的同学，已经看出这就是统计学中的指数平滑。

首先 Alpha 参数为什么要设置到 0.8 - 0.9？

回顾一下 SRTT 的计算方法:

SRTT = (Alpha * SRTT) + ((1-Alpha) * RTT)

可以看出：

• Alpha是历史 SRTT 的权重
• (1-Alpha) 是新测量RTT的权重

当 Alpha=0.8时：

• 80% 是历史 SRTT 的权重
• 20% 是新测量 RTT 的权重

这说明 TCP 更信任历史数据（SRTT），而不是新测量到的 RTT值。

为什么要这样设计？

道理很简单，尽量降低极端异常值对 RTO 的影响，不能 1 次 2 次的高 RTT 延迟，就导致整体 RTO 快速的上升吧。

Alpha 介于 0-1之间，越大，RTT 的曲线越平缓，这也是为什么 Alpha 叫做 平滑因子的原因，画个图直观感受一下：

假设之前的 SRTT = 100 ms，新测量到 RTT = 200 ms

• 如果 Alpha = 0.8 SRTT = 0.8 * 100 + 0.2 * 200 = 120ms
• 如果 Alpha = 0.5 SRTT = 0.5 * 100 + 0.5 * 200 = 150ms

（PS：这种方法可能会在很多场合都会见到，它有个名字：Exponential weighted moving average，中文叫：加权移动平均）

参数 Beta 的作用又是什么呢？

假设测量计算出来的 SRTT 是100ms，如果 RTO 等于SRTT，很容易发生不必要的重传（参考上面的曲线，SRTT 经常会在 RTT 的下方）。

实际的 RTT 会波动，Beta 就是为了应对这种波动，适当把 RTO 设置为 SRTT 的 1-2 倍，尽量多的包含实际 RTT 波动。

推荐值是1.3到2.0

• 1.3：较为激进，适合网络稳定的情况

• 2.0：较为保守，适合网络波动大的情况

LBOUND 和 UBOUND 则分别为上下限，这个很清楚。

但是这种算法，存在一些缺陷：

1. RTT 波动范围问题：

• 小波动场景（RTT 在 100 ms 上下波动 10 ms）
• 大波动场景（RTT 在 100 ms 上下波动 50 ms）
• 虽然 SRTT 相近，但显然需要不同的 RTO策略

如图所示：

2. 对网络突变反应慢：

• 由于采用了平滑计算(Alpha=0.8~0.9)，导致 SRTT 调整过慢

如图所示：

TCP RTO 计算： Jacobson / Karels 算法（RFC6298）

Jacobson/Karels 算法最早由 Van Jacobson 和 Mike Karels 在1988年的论文《Congestion Avoidance and Control》中提出，现已被写入 RFC6298 标准文档。

该算法克服了 RFC 793 中原始算法的缺陷，成为目前 TCP 协议中广泛采用的 RTO 计算方法。

算法原理

该算法采用指数加权移动平均（EWMA）的方法来平滑 RTT 的波动，通过计算 RTT 的偏差来动态调整超时时间，使 RTO 的计算更加准确和灵活。

1. 平滑往返时间（SRTT）

$$
\text{SRTT} = (1 - \alpha) \times \text{SRTT} + \alpha \times \text{RTT}
$$

其中 α = 1/8，这个平滑因子使算法能够在保持对网络变化响应的同时，避免由于瞬时波动导致的剧烈变化。

2. 往返时间偏差（DevRTT）

通过计算实际 RTT 与平滑 SRTT 的偏差，来度量网络延迟的波动程度，同样采用 EWMA 方法，其中 β = 1/4：

$$
\text{DevRTT} = (1 - \beta) \times \text{DevRTT} + \beta \times |\text{RTT} - \text{SRTT}|
$$

3. 超时时间（RTO）

最后，基于 SRTT 和 DevRTT，计算出 RTO：

$$
\text{RTO} = \mu \times \text{SRTT} + \partial \times \text{DevRTT}
$$

其中 μ = 1，∂ = 4，这组参数值是经过大量实验验证的最优经验值，能够在绝大多数网络环境下提供良好的性能（调参工程师）

初始值设置：

• SRTT：在首次测量到 RTT 后，将 SRTT 设置为该测量值。例如，如果第一次 RTT 测量为 100 毫秒，则初始 SRTT = 100 ms。
• DevRTT：初始设定为 SRTT 的一半，以反映初始的不确定性。例如，如果 SRTT = 100 ms，则 DevRTT = 50 ms。

我把这个计算过程画成一个图示:

TCP RTO 计算过程

这里面很多参数是通过实验试出来的，但是我们任然可以通过公式的特点，直观的感受为什么这个公式能适应不同网络特点。

• 假如一个网络耗时很稳定，那是否说明 SRTT 和 RTT 之间的波动很小？

  那么 Dev RTT 就会趋近于 0 ，也就是说最后 RTO 会比较趋于 SRTT（也就是 RTT），对于一个稳定的网络这似乎也符合我们的预期。

• 假如一个网络本来很平稳，突然 RTT 波动剧烈

  那么由于 SRTT 不能及时跟上 RTT 的变化，所以 DevRTT 会快速升高（因为这取决于 RTT 和 SRTT 的差值），最终 RTO 也能快速响应 RTT 的波动变化。

这就是简单从公式定性的角度去理解这个算法的特点：

1. 自适应性强：通过 EWMA 方法，能够自动适应网络状况的变化
2. 抗干扰性好：DevRTT 的引入使算法对网络抖动具有更好的容忍度
3. 实用性高：参数选择经过充分验证，适用于大多数实际场景，现在 TCP 协议中用的就是这个算法

Karn 现象

前面所有 RTO 的计算方法中，往返时间 RTT 的测量都是非常关键的。

但是在发生重传时，由于无法确定收到的ACK是对应原始包还是重传包，因此无法准确计算RTT，这就是著名的Karn现象。

如图所示：

karn 现象

大家看图片会非常清楚 ACK 到底对应哪个原始数据包，但是真实的 TCP包中没有任何的标识，收到 ACK 是完全不知道对应哪个原始数据包的，一般有下图中两种情况:

• 发送方发出的原始数据包在传输过程中丢失（用红色X标记），触发了重传机制。当接收方收到重传的数据包后发回ACK，发送方错误地将这个ACK认作是对原始数据包的确认，从而计算出了一个大于实际值的RTT。
• 发送方发出原始数据包后，由于没有及时收到确认而触发重传，发送了第二个数据包。接收方实际是对最先到达的原始数据包发出的ACK，但发送方错误地认为这个 ACK 是对重传包的响应，导致计算出了一个小于实际值的 RTT

为解决这个问题，Karn提出了一个算法：在计算加权平均往返时间 SRTT 时，不使用发生过重传的报文段的 RTT 样本。

具体来说，当发生重传时，不更新 SRTT 的计算，因此 RTO 也不会更新，这避免了使用不准确的 RTT 样本。

但是，Karn 算法也带来了新的问题：

• 当网络条件发生显著变化，导致报文段的传输时延突然增大并持续较长时间时，由于原有的 RTO 不足以覆盖新的传输时延，会触发重传。而按照 Karn 算法，重传报文段的 RTT 样本不被采用，导致 RTO 无法及时调整以适应新的网络状况。这种情况下，报文段会反复重传，严重影响传输效率。

因此，要对 Karn 算法进行修正，方法是:

报文段每重传一次，就把超时重传时间 RTO增大一些。典型的做法是将新 RTO 的值取为原 RTO 值的 2 倍。

最终整个 RTO 的计算过程如下图:

TCP RTO 计算过程

二、TCP 滑动窗口

在说明 ACK 确认机制的时候，我们说发送方和接收方可以通过 发送-确认 来确保数据都被正确传输。

TCP 基本 ACK 机制

但是如果发送方每次发送完一个数据包就要等收到 ACK 再发下一个数据包的话，效率未免太低，并且速度瓶颈非常明显。

但是如果让发送方一次发送太多的数据包，接收方可能来不及接收或者缓冲区溢出，造成数据丢失。

所以需要进行**流量控制：**也就是让发送方的发送速度不要太快，要和接收方的处理速度相匹配。

而实现流量控制的基础就是 **滑动窗口（Sliding Window）**机制。

滑动窗口机制的实现，依赖于 TCP 头部里的窗口大小字段，该头部是用于接收方告诉发送方接收方的窗口大小，窗口大小字段 16 位，范围为 0~65535字节:

TCP 头部字段

注意：为了扩展接收方窗口大小，TCP 有个扩展字段窗口缩放因子，在三次握手阶段，双方可以协商出这个因子，也就是窗口大小的扩大倍数

2.1 发送方窗口

有了接收方告诉发送方它能接收的数据大小，发送方就可以精准的控制发送的数据包了。

TCP 发送缓冲区示意图

如上图所示，接收方的窗口大小对应也成为了发送方的发送窗口大小。

当应用程序调用 send/write 发送数据时，数据会被写入到 TCP 发送缓冲区中，正是由于发送窗口的存在，整个发送缓冲区的数据可以分为三个部分：

1. 蓝色区域：已确认的数据
   • 这部分数据已经发送并收到 ACK
   • 表示数据已经成功传输，可以从缓冲区中删除了
2. 绿色区域：发送窗口
   • 这部分是当前可以发送的数据区域
   • 由接收方的窗口大小决定
   • 包含"已发送但未确认"和"未发送但可发送"的数据
3. 灰色区域：未发送且不可发送的数据
   • 虽然这些数据已经进入了发送缓冲区
   • 但由于接收方的窗口限制，暂时不能发送
   • 必须等待前面的数据被确认后，窗口才能向右滑动

图中虚线框表示的"发送窗口"，就像一个滑动的窗口一样，当接收方确认了数据后，窗口就可以向右滑动（如图中箭头所示），这样就有更多的数据可以被发送出去。

但是注意，发送窗口内还会细分为：

• 已发送未确认
• 未发送但是可以发送

原因很简单，就是每时每刻窗口可能都会移动，所以这个发送窗口不可能随时都是处于全部发完等待确认的状态，它肯定会有部分发了，部分没发，如图所示(参考TCP/IP Guide示意图绘制)：

TCP滑动窗口

TCP/IP Guide 中 将发送方缓冲区分为四类数据区域：

• Category #1（蓝色区域）：序号小于32的数据，都是已发送并确认的
• Category #2（绿色区域）：序号32-45的数据，已发送但未收到确认
• Category #3（橙色区域）：序号46-51的数据，未发送但在接收方窗口允许范围内
• Category #4（灰色区域）：序号52及以后的数据，未发送且超出接收方窗口范围

发送窗口大小(SND.WND)

• 值为 20 字节
• 这个值是由接收方通知给发送方的
• 表示接收方当前能够接收的最大数据量

还有两个重要的指针位置：

• SND.UNA = 32：表示第一个未确认的字节序号
• SND.NXT = 46：表示下一个要发送的字节序号

可用窗口(Usable Window)：

• 可用窗口大小 = SND.UNA + SND.WND - SND.NXT
• 可用窗口表示发送方还可以发送的字节数据，说人话就是接收方还有空间但是发送方还没发的

非常显然，可用窗口的大小处于 0 和 SND.WND 之间变动，也就是全部都发出去了等待确认的话，可用窗口就是0，如果发送窗口内一个字节都还发，那可用窗口就等于发送窗口 SND.WND。

这种设计的精妙之处在于：

1. 通过 SND.UNA 和 SND.NXT 两个指针，可以准确跟踪数据的发送和确认状态
2. 通过 SND.WND （发送窗口大小） 控制发送速率，实现流量控制
3. 可用窗口大小的动态计算，确保发送方不会发送超过接收方处理能力的数据

当接收方确认数据后，SND.UNA 会右移，窗口就会向右滑动，使得发送方可以发送更多的新数据，这就是"滑动窗口"名称的由来。

滑动窗口非常的简单且优雅，能够实现：

1. 流量控制：接收方可以通过调整窗口大小来控制发送方的发送速率，防止发送太快导致接收方缓冲区溢出
2. 提高效率：发送方不必在每发送一个数据包后等待确认，而是可以连续发送一个窗口的数据

2.2 接收方窗口

刚才我们说发送方的窗口是收到接收方的控制，接收方通过维护一个滑动窗口来告知发送方它的接收能力，从而避免发送方发送过多数据导致接收方缓冲区溢出。

让我们通过这张图详细了解接收方窗口的工作机制：

TCP 接收方缓冲区

两个关键参数控制接收窗口的行为：

• RCV.NXT（32）：表示接收方期望收到的下一个字节序号
• RCV.WND（20字节）：表示接收方当前可以接收的数据量，通常取决于接收方的缓冲区大小，这个数字也会通过 TCP 头部通知给发送方

整个数据流按照处理状态分为三类（和发送方是大概对应的）：

• Category #1+2（已接收并确认）：序号小于 RCV.NXT(32) 的数据都已经被正确接收和确认
• Category #3（允许接收）：序号在 [RCV.NXT, RCV.NXT + RCV.WND) 即 [32, 52) 范围内的数据
• Category #4（暂不接收）：序号大于等于 52 的数据暂时不允许发送方发送

窗口滑动过程：

• 当接收到正确的数据后，RCV.NXT 向右移动
• 接收窗口随之整体右移
• 这使得发送方的 SND. UNA 右移动，这样就可以发送新的数据

接收方窗口机制通过这种设计，既保证了数据传输的可靠性，又实现了基于接收方处理能力的流量控制，是 TCP 协议中一个非常精妙的设计。

接收方会定期将这些窗口信息通告给发送方，发送方则需要严格遵守这些限制，确保发送的数据不会超出接收方的处理能力。

一般来说，发送方指针 SND和接收方指针 RCV 是在动态变化中相等，原因在于数据在网络中传输和处理有时延，包括发送窗口大小和接收方大小窗口大小，也是在动态变化中相等，因为接收方窗口的调整反馈给发送方有一定的延迟。