剑指 Offer 22. 链表中倒数第k个节点

题目

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。

例如，一个链表有 6 个节点，从头节点开始，它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。

示例:

给定一个链表: 1->2->3->4->5, 和 k = 2.

返回链表 4->5.

Leetcode链接:

https://leetcode.cn/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/ (opens new window)

解题思路

遍历解法（双指针）

最简单的肯定是先遍历一遍链表，获得长度 n，倒数第 k 个节点就是第 (n-k) 个节点（这里暂不考虑 k >= n等无效场景）。

还有一种双指针解法，就是让两个节点相距 k 个，然后同时从前往后遍历，当前面那个节点遍历到链表尾部的时候，后面那个节点就恰好在倒数第 K 个元素，如图：

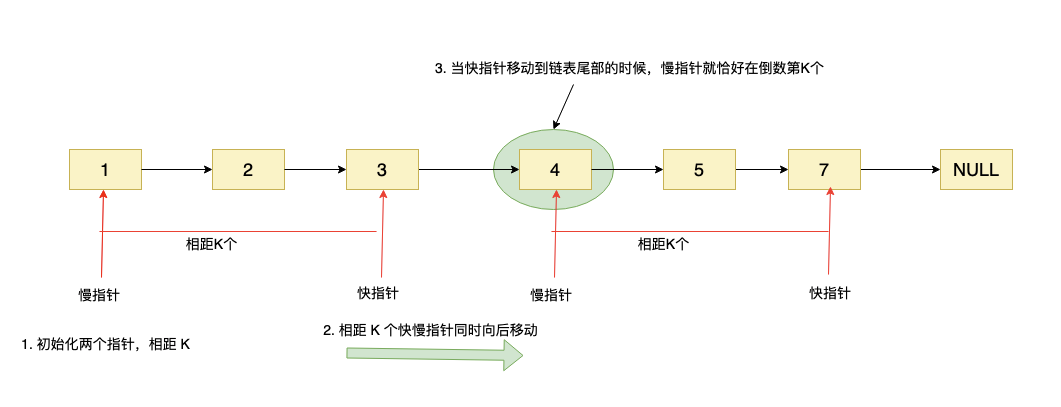
**双指针解法代码: **

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        // 快慢指针，两者相隔 k，如果整个链表长度都不够 k，则返回 空
        ListNode *slow = head;  // 慢指针
        ListNode *fast = head;// 快指针
        // 将 cur 向后移动 k 个
        while(k > 0 && fast != nullptr) {
            fast = fast->next;
            k--;
        }
        
        // 如果 k 不等于0，则说明整个链表长度不足 k (注意代码鲁棒性，做一些边界判断）
        if(k != 0) {
            return nullptr;
        }

        // 然后 快指针和慢指针一起向后移动，快指针为空时，慢指针即为倒数第K个
        while(fast != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

时间复杂度: O(N): 因为只需要遍历一遍链表

空间复杂度: O(1): 常数大小的额外开销

递归解法

为什么会想到递归呢，其实因为要求倒数第K个节点，那么从后往前数其实是最好找的，单链表向后如何做到反向向前呢？

其实就是递归，递归的本质就是不断把问题拆解成更小规模的子问题，当子问题简单到无需再递归时就可以开始返回。

递归题解：

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        ListNode *temp = nullptr;
        getKthFromEnd(head, k,  &temp);
        return temp;
    }
		
   	// 这个方法的返回值是 cur 为头结点时间的子链表长度
    // 那么当子链表的长度为 k-1 时，当前的节点就是倒数第 k 个，head 是二级指针，用来存储找到的倒数第 k 个节点
    int getKthFromEnd(ListNode* cur, int k, ListNode** head) {
      	// 如果cur为空，则以cur为头结点的子链表长度为0，属于递归终止条件
        if(cur == nullptr) {
            return 0;
        }
        // 递归处理下一个 cur->next;
      	// 返回值就是以  cur->next 为头结点的子链表的长度
        int num_from_end = getKthFromEnd(cur->next, k, head);
      
        // 如果子链表长度等于 k-1，则当前节点就是第 k 个，记录到二级指针 head
        if (num_from_end == (k-1)) {
            *head = cur;
        }
     	
        // 以 cur 为头结点的子链表长度 = 以 cur->next为头结点的子链表长度 + 1
        return num_from_end + 1;
    }
};

时间复杂度: O(N): 递归 N 次

空间复杂度: O(N): 递归深度 N * 单次递归常数项辅助空间